Circle of Fifths

Key of C major:

C D E F G A B C

And then calculate the intervals between each note (T=Tone, S= Semitone):

C [T] D [T] E [S] F [T] G [T] A [T] B [S] C

Notice that, without alteration these notes already conform to the major scale formula. So we say that the key of C major has no sharps. A line of music written in this key would start like this:

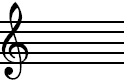
Now count up five steps (because we are following the circle of fifths):

C D E F G

This gives you G major as the next key in the circle. Write out the letters for G:

G A B C D E F G

And then calculate the intervals between each note (T=Tone, S= Semitone):

G [T] A [T] B [S] C [T] D [T] E [S] F [T] G

Now compare this to the major scale formula ( T,T,S,T,T,T,S) and we see that the F note is wrongly positioned (too close to the E and too far from the G).

We fix this by turning the F into F#. So the notes in the key of G major are:

G A B C D E F# G

And we say that the key of G major has ONE SHARP: F#

The start of a line of music written in this key would like this:

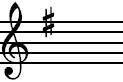
The sharp sign is placed on the top line where the note F would be found.

Now count up five steps again.

G A B C D

This gives you D major as the next key in the circle. Write out the letters for D:

D E F G A B C D

And then calculate the intervals between each note (T=Tone, S= Semitone):

D [T] E [S] F [T] G[T] A [T] B [S] C [T] D

Now compare this to the major scale formula ( T,T,S,T,T,T,S) and we see that both the F note and the C note are wrongly positioned.

We fix this by turning the F into F# and the C into C#. So the notes in the key of D major are:

D E F# G A B C# D

And we say that the key of D major has TWO SHARPS: F# and C#

The start of a line of music written in this key would like this:

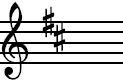
The new sharp sign is placed on the third space up where the note C would be found.

Now count up five steps again.

D E F G A

This gives you A major as the next key in the circle. Write out the letters for A:

A B C D E F G A

And then calculate the intervals between each note (T=Tone, S= Semitone):

A [T] B [S] C [T] D [T] E [S] F [T] G[T] A

Now compare this to the major scale formula ( T,T,S,T,T,T,S) and we see that the F note, the C note and the G note are all wrongly positioned.

We fix this by turning the F into F#, the C into C# and the G into G#. So the notes in the key of A major are:

A B C# D E F# G# A

And we say that the key of A major has THREE SHARPS: F#, C# and G#

The start of a line of music written in this key would like this:

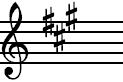
The new sharp sign is placed above the top line where the note G would be found.

At this stage it is worth pausing to see what the pattern is that develops as we work round this circle of fifths. If we retrace our steps we can see that we are following these rules:

1. The new key in the circle is based on the note five steps above the previous key.
2. Each key in the circle keeps the #s that were added in all previous keys.
3. One new sharp is added at each step in the circle and this new sharp is always note 7 in the key.

So lets see if we can speed up the process by using these three rules as shortcuts:

We were up to the key of A major so according to rule 1. the next key will be E major.

Rule 2. tells us that the notes F, C and G will all be sharped and rule 3. says that D will be sharped as well (D is note 7 in the key of E).

So, by applying the rules we calculate that the key of E major comprises:

E F# G# A B C# D# E

Let’s just check by examining the intervals between each note:
E [T] F# [T] G# [S] A [T] B [T] C# [T] D# [S] E

T T S T T T S which checks out against our major scale formula. So we know the system works!

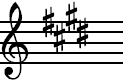
The new sharp sign is placed on the fourth line where the note D would be found.

We can predict that the next key in the circle will be B major and that this will have 5 sharps:

B C# D# E F# G# A# B

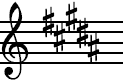
The new sharp sign is placed on the second space up where the note A would be found.

Something a bit strange happens with the next key in the circle. The fifth note in the key of B major is F# so F# major is our next key and as well as the five sharps inherited from B major, if we follow our rules we will want to add in E#:

F# G# A# B C# D# E# F#

At first this seems confusing because there isn’t an E# is there? In fact E# is just another name for F. But remember the rule: only one of each letter allowed in a major scale. We can’t have F# and F in the same key. So we use E# as a name for the note that sounds like F.

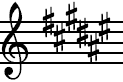
The new sharp sign is placed on the top space up where the note E would be found.

Then we come to the key of C# major with its 7 sharps:

C# D# E# F# G# A# B# C#

This time we have the weirdly named B# which sounds just like the note C, but we can’t call it C in a key that has the note C#.

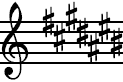
The new sharp sign is placed on the middle line where the note B would be found.

If we move on to complete the circle of fifths we bump into the mysterious world of keys with double sharps!

Bookmark this page:
delicious digg reddit facebook stumbleupon bebo my space live spaces